Исследование функции: примеры решений
На этой странице мы разберем пошагово, как выглядит решение задачи исследования функции с помощью производной, пройдем по всем шагам алгоритма, проведем вычисления и построим итоговый график.
Вы найдете решения практически для всех возможных типов функций, встречающихся в учебных заданиях - от многочленов и дробей до экспонент, логарифмов и кусочно-заданных функций.
Полный пример решения онлайн
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя. $$1-x=0, \quad \Rightarrow \quad x=1.$$ Исключаем единственную точку $x=1$ из области определения функции и получаем: $$ D(y)=(-\infty; 1) \cup (1;+\infty). $$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
![]()
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ - вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x \in (-\infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x \in (1; +\infty)$ функция $y\lt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
![]()
5) Исследуем функцию на периодичность. Функция не является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
![]()
![]()
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y'=0$):
![]()
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
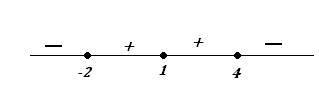
При $x \in (-\infty; -2), (4;+\infty)$ производная $y' \lt 0$, поэтому функция убывает на данных промежутках.
При $x \in (-2; 1), (1;4)$ производная $y' >0$, функция возрастает на данных промежутках.
При этом $x=-2$ - точка локального минимума (функция убывает, а потом возрастает), $x=4$ - точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
![]()
![]()
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x \in (-\infty; 1)$ выполняется $y'' \gt 0$, то есть функция вогнутая, когда $x \in (1;+\infty)$ выполняется $y'' \lt 0$, то есть функция выпуклая.
8) Исследуем поведение функции на бесконечности, то есть при ![]() .
.
![]()
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
![]()
![]()
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
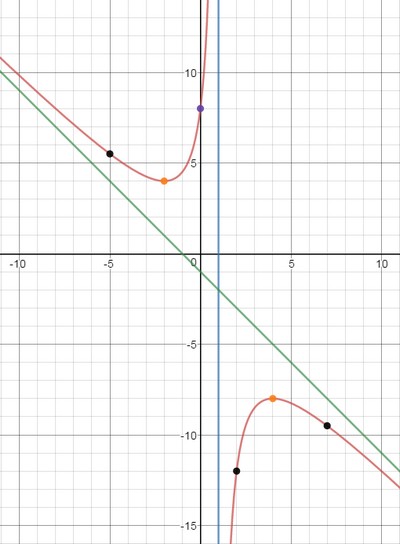
$$ y(-5)=5.5; \quad y(2)=-12; \quad y(7)=-9.5. $$10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Общая схема исследования функции
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
Многочлены
Задача. Исследовать функцию и построить ее график.
$$y=-\frac{1}{4}(x^3-3x^2+4).$$Задача. Исследовать с помощью производных функцию, построить график.
$$y=x^3-3x+2.$$Задача. Исследовать функцию и построить ее график.
$$y=(x-5)(x-3)^3.$$Дробно-рациональные функции
Задача. Исследовать функцию c помощью производных и построить ее график.
$$y=\frac{x^2-x+4}{2x}.$$Задача. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=\frac{x^3-1}{4x^2}.$$Задача. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=\frac{x^3}{x^2-1}.$$Задача. Проведите исследование функции с построением графика.
$$y=\frac{x^3}{2(x+5)^2}.$$Задача. Проведите исследование функции с построением графика.
$$y=\frac{x^3}{4-x^2}.$$Задача. Исследовать функцию и построить ее график.
$$y=\frac{-9x-2}{x^2-8x+16}.$$Задача. Исследовать функцию с помощью производных, и построить график на основании результатов исследования.
$$y=\frac{2x-x^3}{(4-x^2)(x+1)}.$$Иррациональные функции
Задача. Провести полное исследование функции и построить график.
$$y=\frac{x}{\sqrt{x^2+x}}.$$Задача. Проведите исследование функции с построением графика.
$$y=\sqrt[3]{x^2(x+4)}.$$Функции с экспонентой
Задача. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=\frac{e^x}{x}.$$Задача. Исследовать функцию и построить ее график.
$$y=x^2 e^{-\frac{x^2}{2}}.$$Функции с логарифмом
Задача. Исследовать функцию с помощью производной и построить график.
$$y=\ln \frac{x+1}{x+2}.$$Задача. Исследовать функцию и построить ее график.
$$y=\ln(4-x^2).$$Тригометрические функции
Задача. Провести полное исследование периодической функции $y = \cos 3x – 2 \sin 6x$ и построить её график.
Задача. Исследовать функцию и построить ее график.
$$y=x-\arctan(2x).$$Сложные функции
Задача. Провести полное исследование и построить график функции.
$$f(x)=\frac{x}{2}-\arccos\frac{2x}{1+x^2}.$$Задача. Исследовать функцию и построить ее график.
$$y=x^{1/x}.$$Другие задачи на исследование функций
Задача. Построить график функции $y=y(x)$, заданной параметрически
$$x=\frac{t^2}{t+1}, y=\frac{1}{t}-\frac{t^3}{3}.$$Задача. Исследовать функцию и построить ее график $r=1+tg \phi$.
Задача. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача. Исследовать функцию. Построить эскиз графика функции.
\[ y = \begin{cases} -1{,}5 \sqrt{(x - 1)^2} - 1{,}5x + 1{,}5, & x \leq 2 \\ \frac{2}{x - 2} + x - 2, & x > 2 \end{cases} \]Задача. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=\frac{4-x^3}{x^2}.$$
