Исследование функции и построение графика
Эта страница — ваш пошаговый навигатор по исследованию функций. Вместо того чтобы теряться в справочниках и видео, вы получите стройный алгоритм, наглядные примеры для разных типов функций, ссылки на проверенные сайты и методички. Учитесь не просто строить график, а понимать, почему он выглядит именно так, а примеры вам помогут.
Что будет дальше?
Общая схема исследования
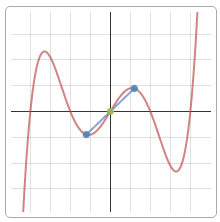
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены "горбы" выпуклости, где не определены значения и т.п.
А уже на основании этих "особенностей" и строится макет графика - картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Часто задачу формулируют как исследовать функцию с помощью производной, и это непроста. Важно хорошо уметь вычислять пределы и находить производные — без этого анализ не выйдет:(. Если у вас есть пробелы в этих темах, начните с разбора наших примеров по непрерывности, пределам и производным.
Алгоритм исследования
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат и промежутки знакопостоянства.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график функции, ее асимптот, отметить ключевые точки.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте эти требования при оформлении решения.
Подробное описание шагов исследования функции
Каталог примеров решений
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения). Мы собрали примеры из контрольных на исследование функций наиболее часто встречающихся типов и вынесли на отдельную страницу примеров (кнопки кликабельны).
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Невероятно гибкий и функциональный графический калькулятор Desmos. Интуитивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=\frac{x^3}{4(x-2)^2}$ буквально за минуту можно построить основной график и асимптоты:
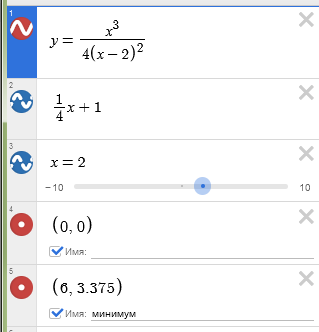
Отмечены и важные точки на графике: локальный экстремум, пересечение с осями.
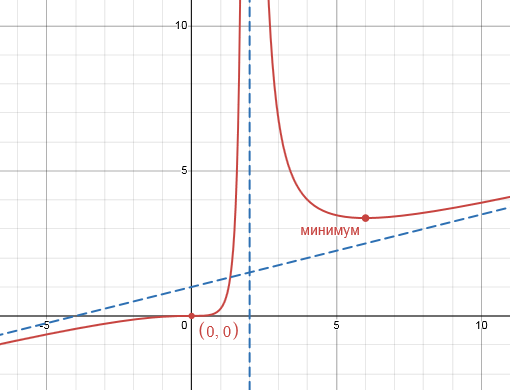
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Как легко построить график функции в Desmos
Графический калькулятор GeoGebra
Сайт GeoGebra также представляет бесплатный доступ к мощному графическому калькулятору. Интерфейс частично похож на Десмос (настройки отображения еще более глубокие + дополнительные инструменты). Рассмотрим для наглядности все ту же функцию: $y(x)=\frac{x^3}{4(x-2)^2}$. Вводим в список функцию, уравнения асимптот и точки:

Получаем график с отметками и асимптотами:
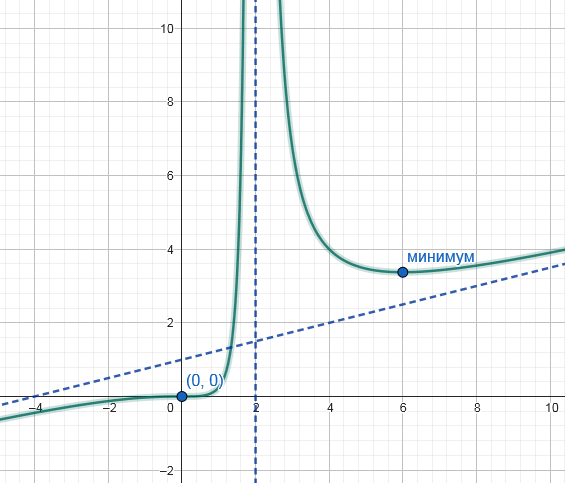
Сайт для построения графиков y(x).ru
Рассмотрим еще один сайт с более простым функционалом: y(x).ru. Это российский продукт, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
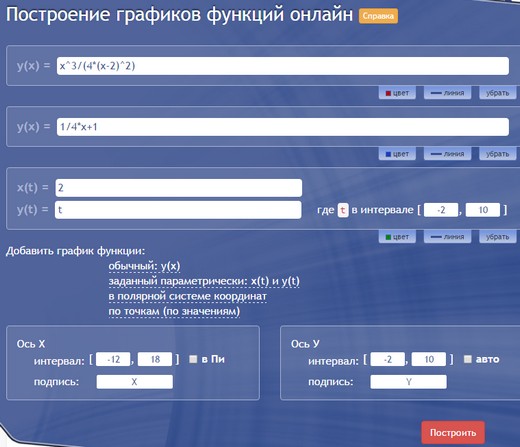
И такой график получается в итоге:
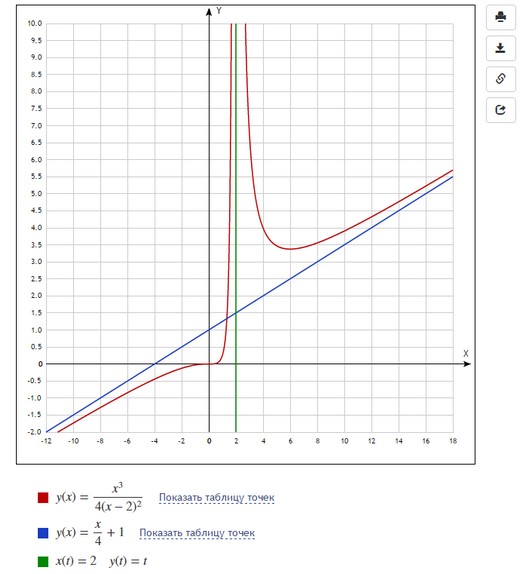
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты для построения графиков онлайн
Еще несколько бесплатных онлайн-сервисов, которые обладают меньшим удобством или функциональностью, но тоже достойны внимания:
- mathway.com Графический калькулятор со списком выражений (а-ля Десмос), есть удобная клавиатура для ввода. Можно строить много графиков одновременно, настраивать цвет, отображать дополнительно точки, настраивать масштаб.
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет.
Обзор онлайн-сервисов для полного исследования функций
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему полного исследования функции
Онлайн-изучение темы "на пальцах"
Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень "съедобно" даже для полного чайника в математике:
Исследование функций от Александра Емелина.
Хорошая методичка с теорией и примерами
Д.Л. Белоцерковский ПОЛНОЕ ИССЛЕДОВАНИЕ ФУНКЦИИ, методические указания, М., 2014 (РГУ нефти и газа им. И.М. Губкина). 33 страницы. В файле вы найдете теорию по теме, полный разбор шести функций, советы по построению графиков в Mathematica, и РГР с 60 вариантами.
Полезные видео-уроки
Последовательный видео-пример, в котором автор исследует функцию $y=x^4/(x^3-1)$ и сопровождает это своими комментариями. Условно, это как читать готовые решения, но тут еще вслух и с дополнительными пояснениями. На начальном этапе это более эффективный способ (чем чтение), чтобы понять тему исследования функции.
Плейлист из 7 видеоуроков по исследованию функции с помощью производной. Вы можете посмотреть все подряд, чтобы хорошо разобраться в теме, или выбрать только ту, где есть пробелы, скажем, про асимптоты или выпуклость.
Лекция по высшей математике на тему исследования функции с помощью производной.

