Как построить график функции онлайн
На этой странице мы разберем пошагово, как построить график любой функции, которую вы исследуете с помощью производной, или используете для решения других математических задач.
Мы будем использовать бесплатный графический калькулятор Desmos.com. Разберем основные функции, которые пригодятся для построения графика функции, асимптот, ключевых точек и т.п.
Построение графика многочлена онлайн
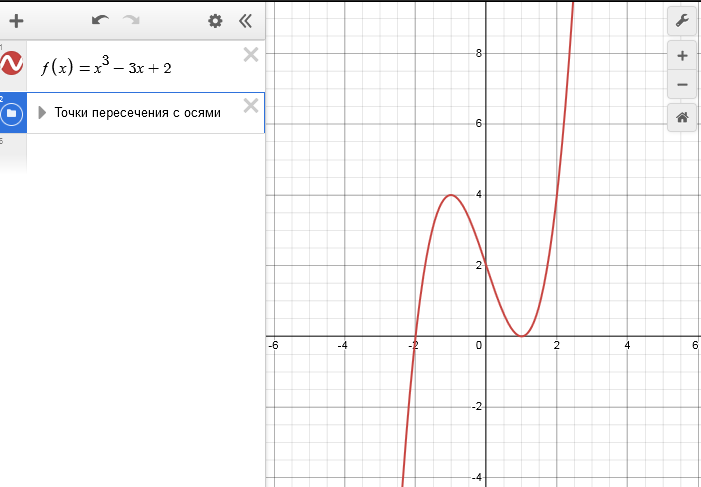
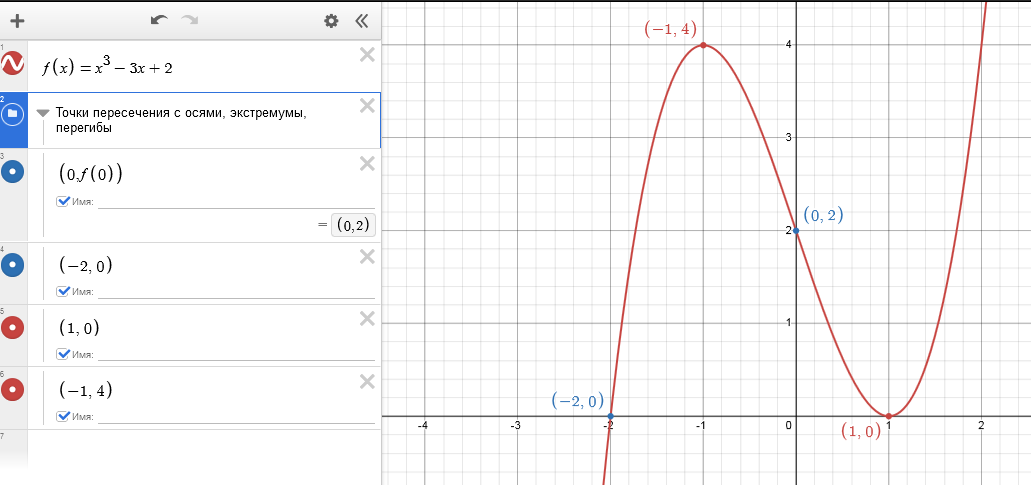
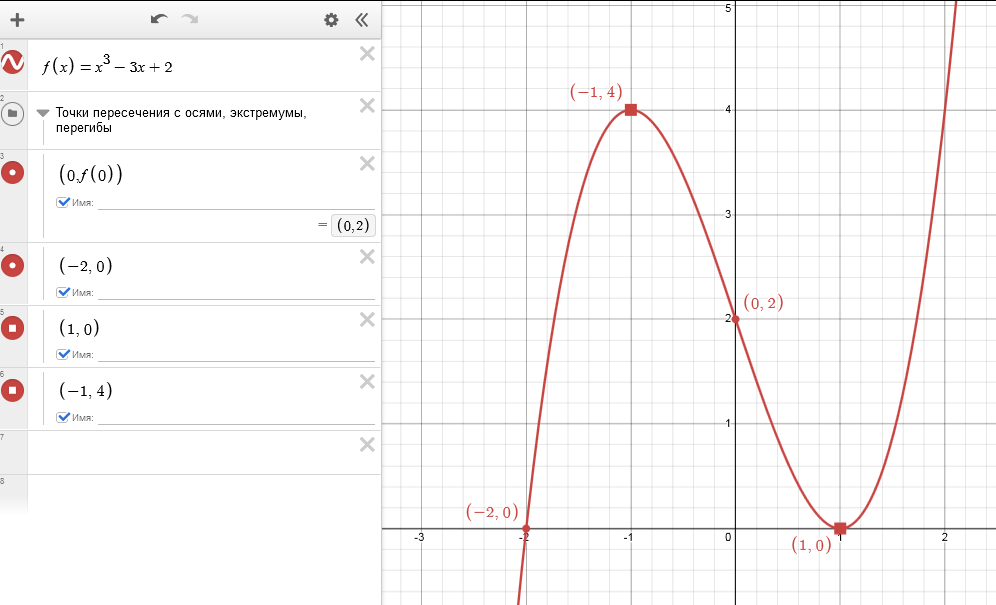
Начнем с простой функции - многочлена. Дана функция $y=x^3-3x+2$ (полное исследование этой функции). Построим пошагово график.
Переходим на сайт Desmos и вводим в поле слева (это называется "Список выражений") уравнение функции - и сразу получаем справа построенный график функции:
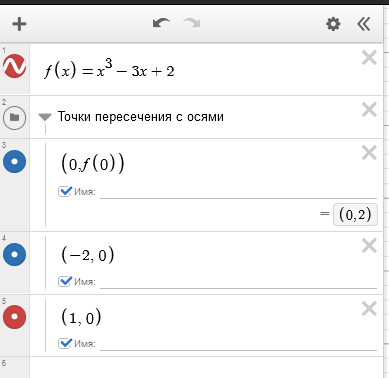
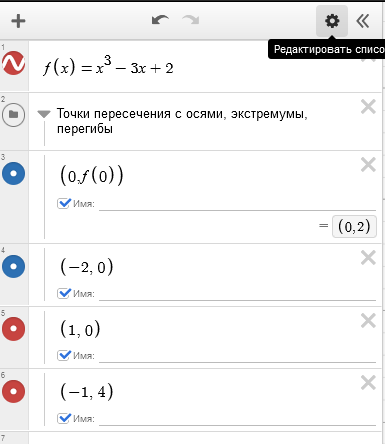
Отметим на нем точки пересечения с осями координат. Можно просто навести курсор на требуемое место (важные точки подсвечиваются серым на графике), кликнуть на иконку 
("Экспортировать точку в список выражений"), и точка появятся в таблице. Проставленная галочка "Имя" поможет подписать координаты прямо на графике. Или можно просто вводить координаты точек в список выражений (в круглых скобках,через запятую):
Для случая $x=0$ мы можем дать команду для вычисления координат точки следующим образом: $(0, f(0))$ и калькулятор сам вычислит значение: $(0,2).$
Вид команд для отображения точек пересечения, Desmos
Вид графика с точками пересечения, Desmos
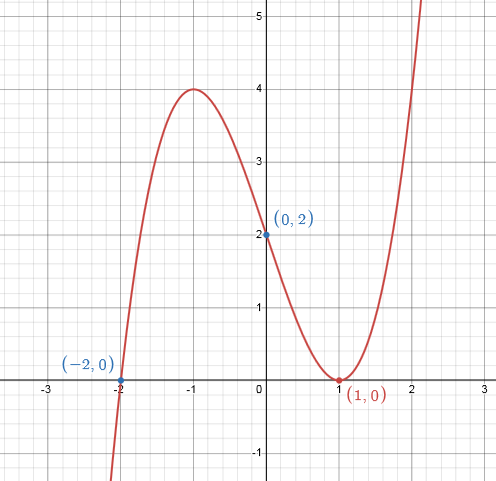
Теперь отметим точки экстремумов, найденные в при исследовании функции (они же хорошо видны на графике - достигаются в точках $(1,0)$, $(-1,4)$) и точку перегиба $(0,2)$. Две из них уже были на графике, выделим последнюю:
Как добавить точку в список команд, Desmos
Вид графика с ключевыми точками, Desmos
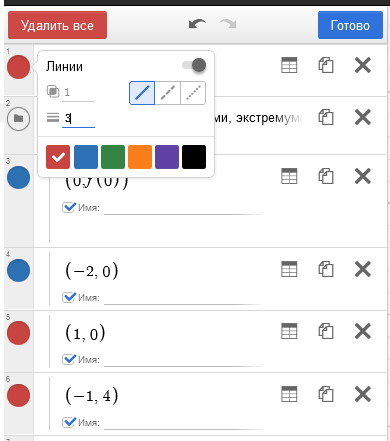
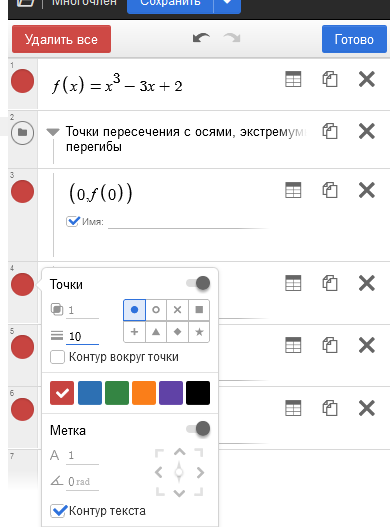
Осталось немного "навести красоту", например, сделать график пожирнее, точки все одного цвета, а для максимума и минимума сделать маркеры-квадраты. Для этого используем настройки отображения. Кликнем на шестеренку над списком выражений, после чего список перейдет в режим настройки отображения. Кликая на цветной кружок слева от объекта, открываем меню, где можно выбрать нужный цвет, толщину, маркер и т.п. (см. ниже в галерее):
Переход в режим настроек отображения объектов, Desmos
Настройка отображения линии, Desmos
Настройка отображения точки, Desmos
Итоговый график многочлена, Desmos
Ссылка на график функции $y=x^3-3x+2$
График дробно-рациональной функции онлайн
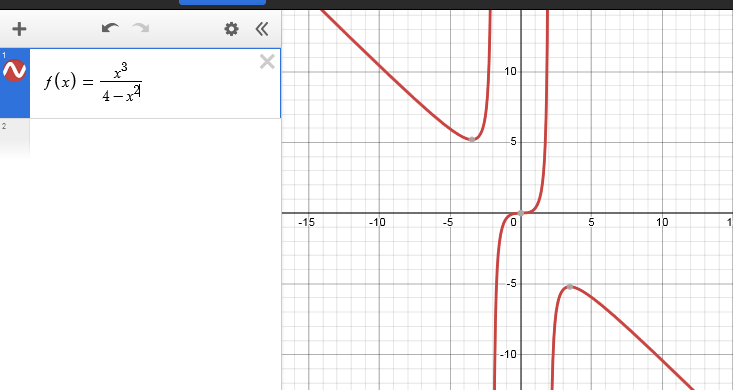
Перейдем к функции немного посложнее (тут её полное исследование):
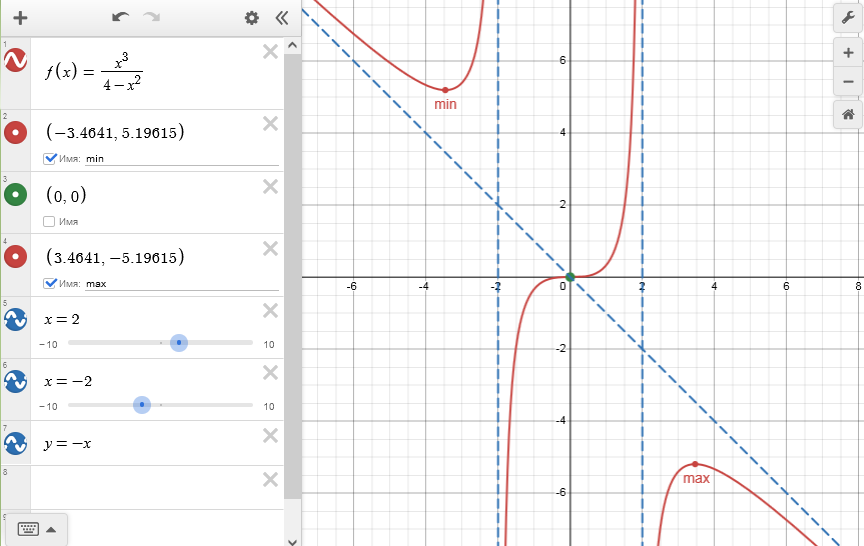
$$ y=f(x)=\frac{x^3}{4-x^2} $$Начнем с того, что введем в список выражений слева формулу для функции:
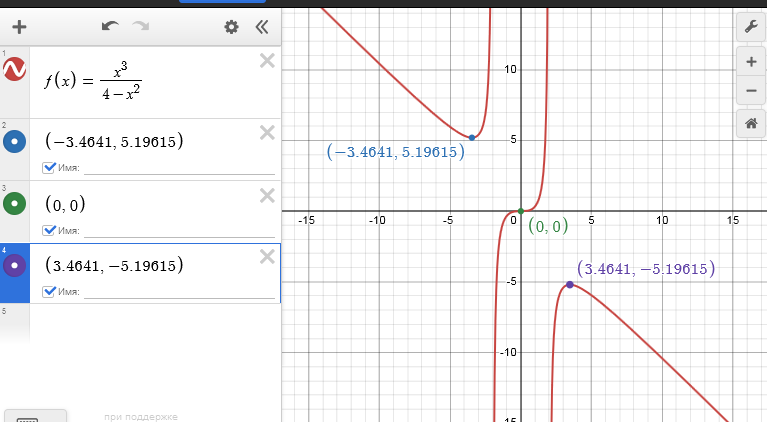
Отлично! Уже виден график, плюс подсвечены серым ключевые точки (это точка пересечения с осями координат, а также минимум и максимум). Кликнем на них и поставим галочки "Имя", чтобы наглядно отобразить координаты на графике:
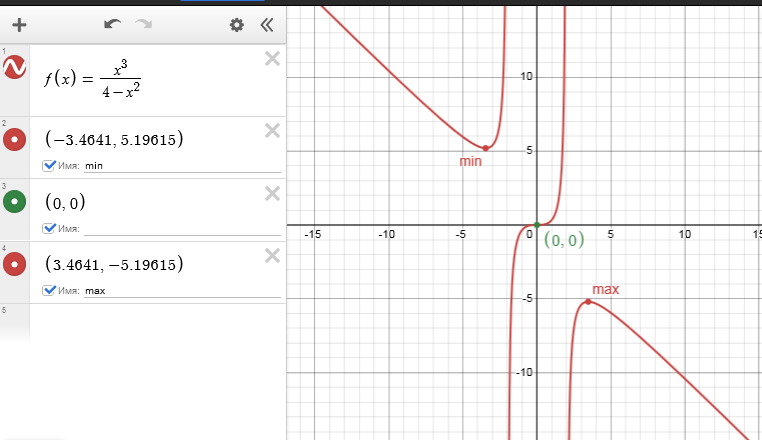
Для этой функции значения дробные, "некрасивые", поэтому тут нагляднее использовать в качестве метки не координаты, а обозначения точек - подпишем их как min и max, а также поменяем цвет:
У данной функции есть и асимптоты, построим их, вводя последовательно выражения для них: $x=-2$, $x=2$, $y=-x$. Чтобы отличать их от графика самой функции, выберем для каждой асимптоты синий цвет и отображение пунктирной линией:
Смена отображения для асимптот, Desmos
Дробно-рациональная функция, итоговый график, Desmos
Ссылка на график функции $y=\frac{x^3}{4-x^2}$
График иррациональной функции онлайн
Рассмотрим функцию с кубическим корнем (тут её полное исследование):
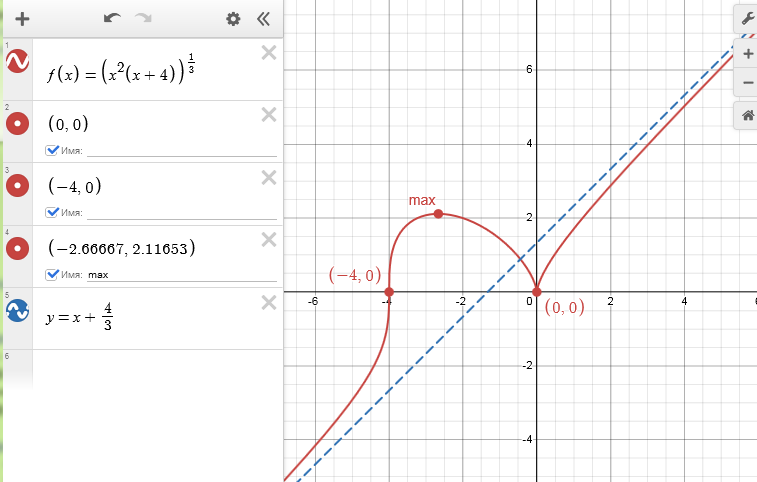
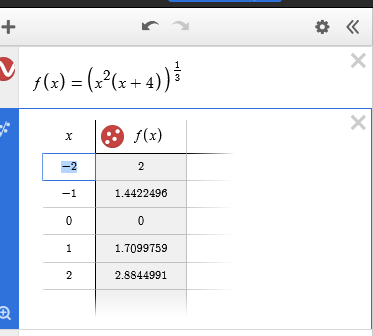
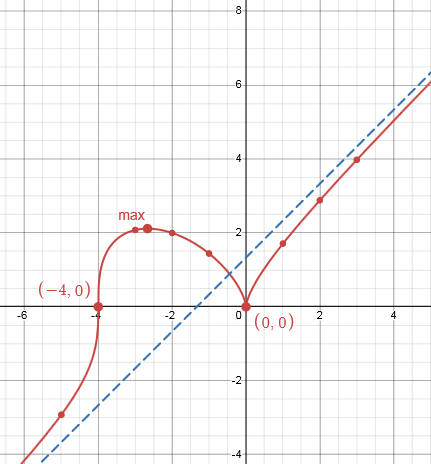
$$ y=f(x)=\sqrt[3]{x^2(x+4)} $$Введем в список выражений слева формулу для функции (корень можно ввести как степень "1/3"). Далее, как делали выше, отметим прямо на графике или введем вручную ключевые точки: пересечения с осями, максимум и минимум. Построим наклонную асимптоту $y=x+4/3$. График сразу приобретет наглядный вид:
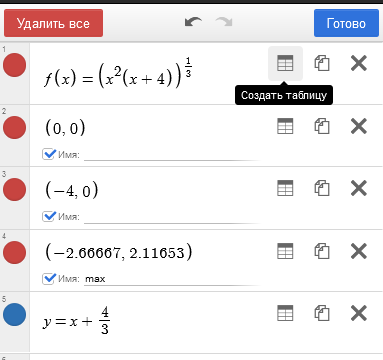
Предположим, что нужно найти дополнительные точки для построения графика, это очень легко сделать в Desmos. Продемонстрируем на нашем примере. Нажимаем вверху слева на значок шестеренки и выбираем значок с таблицей возле функции (подсказка "Создать таблицу"). Кликаем и получаем автоматически таблицу значений в точках от -2 до 2 с шагом 1:
Построить таблицу точек для функции, Desmos
Таблица точек для функции, Desmos
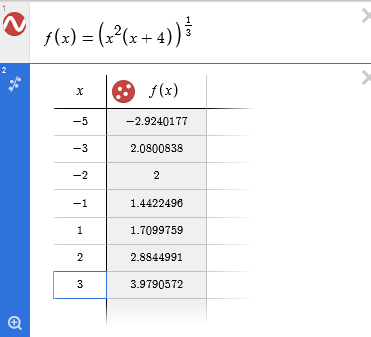
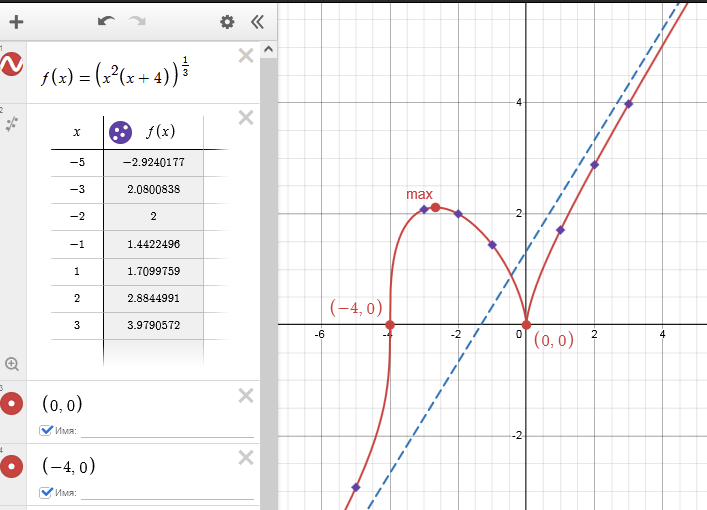
Заменим значения в таблице на те, что нужны нам для графика, возьмем, например, $x=-5$, $x=-3$ и т.п., см. на рисунке ниже. Подбираем те точки, которые еще неизвестны, но удобны для построения (особенно если переносите график на тетрадный лист вручную), а Desmos вычисляет значения функции в них автоматически и отобразит на графике (см. в галерее):
Новые точки в таблице функции, Desmos
Иррациональная функция, итоговый график, Desmos
Если нужно, можно отключить дополнительные точки (скрыть их отображение, нажав на цветной кружок в таблице), или, скажем, поменять им цвет для наглядности (ниже выбрала фиолетовые маркеры):
Ссылка на график функции $y=\sqrt[3]{x^2(x+4)}$
График кусочно-заданной функции онлайн
Рассмотрим функцию, которая задана на разных интервалах разными формулами (кусочно-задана) (полное исследование):
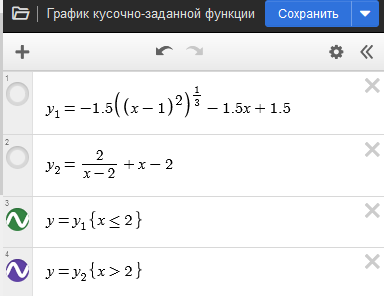
\[ y = \begin{cases} -1{,}5 \sqrt{(x - 1)^2} - 1{,}5x + 1{,}5, & x \leq 2 \\ \frac{2}{x - 2} + x - 2, & x > 2 \end{cases} \]Desmos позволяет строить графики таких функций. Самый простой способ - это ввести две функции, для каждой в фигурных скобках после нее указать ограничения на $x$ (для удобства обозначим на каждом интервале функцию за $y_1$, $y_2$:
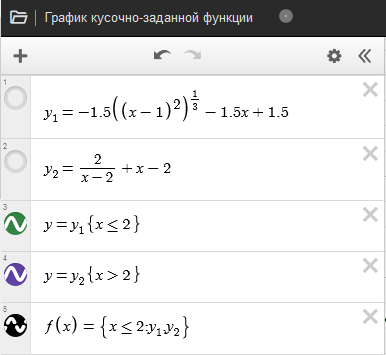
Функцию можно задать и одним выражением следующим образом $f\left(x\right)=\left\{x\le2:y_{1},y_{2}\right\}$:
В фигурных скобках сначала нужно указать интервал, потом через двоеточие - формулу для этого интервала, потом можно снова указать интервал - и формулу для функции на этом интервале, последнее значение в этом списке - то, которое функция принимает на оставшихся точках числовой оси (например, для трех интервалов формула примет вид):
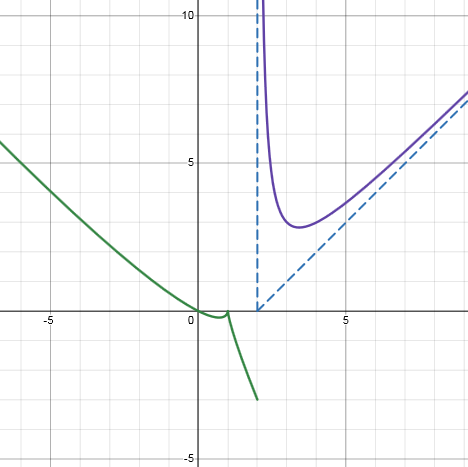
$$ f\left(x\right)=\left\{a_1\le x\le b_1:y_{1}, a_2\le x\le b_2:y_{2}, a_3\le x\le b_3:y_{3}\right\}. $$В нашем случае функция задана всего на двух интервалах, поэтому формула такая короткая. Посмотрим, как выглядит график (добавим сразу обе асимптоты $x=2$, $y=x-2$):
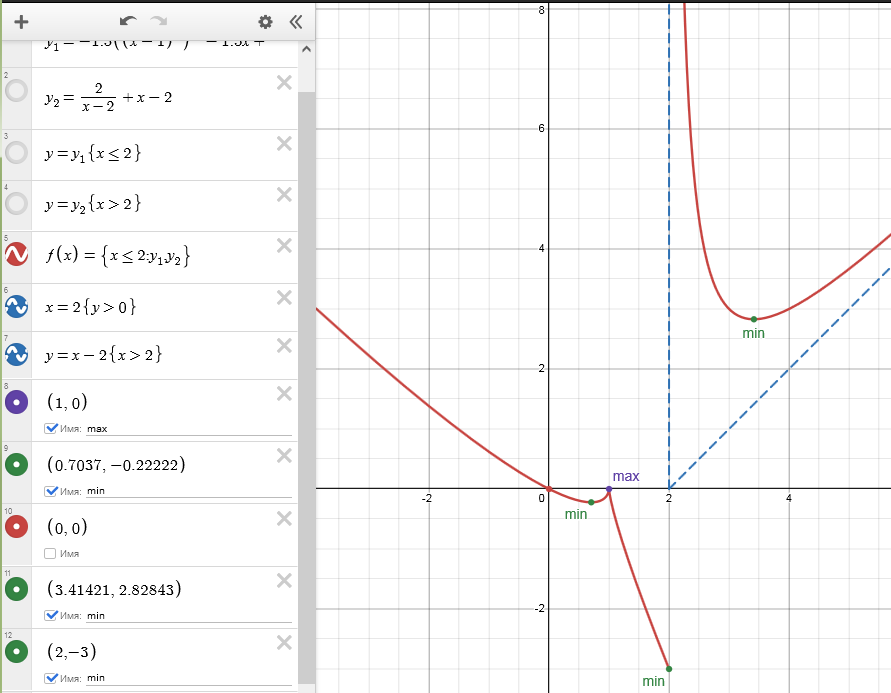
Вернемся к единому цвету графика функции и отметим ключевые точки (экстремумы и точку пересечения с осями координат):
Ссылка на график данной функции в Desmos
Построение графика вашей функции онлайн
Если вы попробовали повторить построения графиков (можно использовать ссылки на готовые листы Десмос после каждой функции, поменять в них что-то, поэкспериментировать), то сможете легко строить и свои функции онлайн.
Вводите свою функцию в списке выражений ниже (слева), чтобы попробовать функции Десмос (сейчас там введена $y=x^2-4$ для примера):