Готовые контрольные по теории вероятностей
На этой странице вы найдете несколько работ, выполненных специалистами МатБюро для студентов разных направлений — как очной, так и заочной формы обучения. Здесь представлены контрольные по теории вероятностей для технических и экономических специальностей, с заданиями разного уровня сложности.
Мы оформляем решения в формате Word — аккуратно, с пояснениями, промежуточными вычислениями, понятными графиками и таблицами. Набираем формулы в редакторе формул и даем краткие комментарии, чтобы было проще разобраться.
Каждая работа делается индивидуально, с учетом методических требований вуза и специфики задач. Ниже вы можете посмотреть, как именно выглядят готовые задания, прежде чем оставить заявку.
Решенные контрольные по ТВ
Контрольная по теории вероятностей 1
Темы: классическая вероятность, геометрическая вероятность, теоремы сложения и умножения, формула Байеса, формула Бернулли
Задача 1. В партии из 25 изделий содержится 15 изделий первого сорта и 10 – второго. Случайным образом выбираются 3 изделия. Найти вероятность того, что среди выбранных хотя бы одно изделие первого сорта.
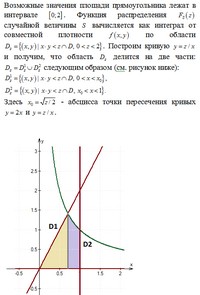
Задача 2. На отрезке наудачу выбраны два числа x и y. Найдите вероятность того, что эти числа удовлетворяют неравенству $x^2 \le 4y \le 4x$.
Задача 3. Дана схема включения элементов. Вероятность отказа каждого элемента в течение времени Т равна 0,5. Вычислить вероятность отказа всей цепи.
Задача 4. Детали изготавливаются на двух станках. На первом станке – 40%, на втором – 60%. Среди деталей, изготовленных на первом станке, брак составляет 2%, на втором – 1,5%. Для контроля случайным образом взята 1 деталь. Найти вероятность событий:
А) деталь бракованная,
Б) деталь изготовлена на 1 станке, если при проверке она оказалась не бракованной.
Задача 5. Прибор проходит независимые испытания. Вероятность выхода из строя прибора при одном испытании равна 0,2. Испытано независимо 100 приборов. Найти вероятность выхода из строя не более одного прибора.
Открыть решение контрольной работы 1 (4 стр.)Контрольная по теории вероятностей 2
Темы: дискретная случайная величина и ее характеристики, непрерывная случайная величина и ее характеристики, нормальный закон распределения, закон Пуассона.
Задача 1. Некто заполнил карточку спортивной лотереи «6 из 49». Случайная величина X – число угаданных им номеров при розыгрыше.
1) составить таблицу распределения случайной величины X;
2) построить многоугольник распределения;
3) найти функцию распределения и построить её график;
4) найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X;
5) найти вероятность P(X>2).
Задача 2. Непрерывная случайная величина X задана с помощью функции распределения:
1. найти неизвестные коэффициенты;
2. построить график функции распределения;
3. найти функцию плотности вероятностей и построить её график;
4. найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X;
5. найти вероятность $P(X\lt 2)$.
Задача 3. Непрерывная случайная величина X задана с помощью функции плотности распределения:
1. найти неизвестные коэффициенты;
2. построить график функции плотности вероятностей;
3. найти функцию распределения и построить её график;
4. найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X;
5. найти вероятность $P(X\gt 1)$.
Задача 4. Заданы функция плотности нормального распределения и интервал (-5;1).
1. найти математическое ожидание m;
2. найти среднее квадратическое отклонение и дисперсию D;
3. найти неизвестный коэффициент А;
4. найти вероятность попадания случайной величины в заданный интервал;
5. построить график функции плотности и на нём отметить площадь, равную найденной вероятности.
Задача 5. Число потерь самолётов в эскадрильи в ходе военной операции определённой сложности подчиняется закону распределения Пуассона. Найти вероятность того, что в предстоящей операции потери будут ниже среднего, если последнее составляет для данного вида операций 7 самолётов.
Открыть решение контрольной работы 2 (9 стр.)Контрольная по теории вероятностей 3
Темы: классическая вероятность, формула полной вероятности, ДСВ, нормальное распределение, линейная регрессия.
Задача 1. В партии из 16 изделий 6 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 5 изделий 3 изделия являются дефектными?
Задача 2. В магазине выставлены для продажи 17 изделий, среди которых 6 изделий некачественные. Какова вероятность того, что взятые случайным образом 3 изделия будут некачественными?
Задача 3. На сборочное предприятие поступили однотипные комплектующие с трёх заводов в количестве: 15 с первого завода, 25 со второго, 20 с третьего. Вероятность качественного изготовления изделий на первом заводе 0.8, на втором 0.7, на третьем 0.9. Какова вероятность того, что взятое случайным образом изделие будет качественным?
Задача 4. Дано распределение дискретной случайное величины X. Найти математическое ожидание и среднее квадратичное отклонение.
Задача 5. В городе имеются 3 оптовые базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0.24. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
Задача 6. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно $M_x=38$, среднее квадратичное отклонение равно $σ_x=2$. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (35;40).
Задача 7. Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины.
Открыть решение контрольной работы 3 (6 стр.)Контрольная по теории вероятностей 4
Темы: вычисление вероятностей событий, дискретные и непрерывные случайные величины, законы распределения.
Задача 1. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 5; б) произведение числа очков не превосходит 3; в) произведение числа очков делится на 4.
Задача 2. На отдельных карточках написаны цифры от 1 до 12. Все карточки перемешиваются, после чего наугад берут пять из них и раскладывают в ряд друг за другом в порядке появления. Какова вероятность того, что при этом получится число 54321?
Задача 3. В группе 15 мальчиков и 10 девочек. Для тестирования случайным образом отобраны 8 детей. Найти вероятность того, что: а) все они - мальчики; б) среди них 3 мальчика.
Задача 4. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка – 0.9; для второго – 0.8; для третьего – 0.85. Найти: а) вероятность того, что в течение некоторого часа ни один станок не потребует к себе внимания рабочего; б) вероятность того, что по крайней мере один из трёх станков не потребует к себе внимания рабочего в течение часа.
Задача 5. Вероятность того, что цель поражена при одном выстреле первым стрелком, равна 0.57, вторым – 0.72. Первый сделал 2, второй - 4 выстрела. Определить вероятность того что цель не поражена.
Задача 6. Рыбак имеет три места для ловли рыбы, которое он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, рыба клюёт с вероятностью 0.4, на втором месте – 0.35; на третьем – 0.45. Рыбак вышел на рыбалку. Какова вероятность того, что рыба клюнула? Известно, что рыбак, выйдя на ловлю рыбы, закинул удочку, и рыба клюнула. Найти вероятность того, что он удил рыбу: а) на первом месте; б) на втором месте; в) на третьем месте.
Задача 7. В библиотеку университета поступила партия учебной литературы, 30% которой составляет литература по гуманитарным дисциплинам, остальные - по естественным. Найти вероятность того, что: а) среди 9 книг данной партии 4 окажется по естественным; б) среди 8 книг окажется от 4 до 7 книг по гуманитарным; в) из 25 книг окажется 10 по естественным; г) среди 200 книг окажется от 60 до 100 учебников по гуманитарным дисциплинам.
Задача 8. Выбиваемые двумя стрелками числа очков характеризуются следующими законами распределения для первого стрелка:... и для второго стрелка:... Стрелки делают по одному выстрелу. Подсчитывается сумма выбитых ими очков.
1) Составить закон распределения этой случайной величины.
2) Проверить равенства
Задача 9. Случайная величина задана функцией распределения... Найти: а) плотность распределения f(x); б) M(X) и D(X); в) построить графики F(x) и f(x).
Задача 10. Случайная величина задана плотностью распределения... Требуется: а) определить коэффициент a; б) найти функцию распределения F(x); в) найти вероятность попадания случайной величины на участок (1;4]; г) построить графики F(x) и f(x).
Задача 11. Результаты измерения расстояния между населёнными пунктами подчинены нормальному закону с параметрами M(X)=16 км, σ(X)=100 м. Найти вероятность того, что расстояние между этими пунктами: а) не меньше 15.8 км; б) находится в интервале (15.8;16.4).
Задача 12. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение (по формулам и непосредственно по определению) случайной величины, распределённой равномерно в интервале [2;7].
Открыть решение контрольной работы 4 (15 стр.)Часто задаваемые вопросы
Какие темы обычно входят в контрольные по ТВ?
Наиболее часто встречаются задачи на темы: комбинаторика, классическое и геометрическое определение вероятности, независимые события, формулы Байеса и полной вероятности, схема независимых испытаний Бернулли, формулы Лапласа и Пуассона, дискретные и непрерывные случайные величины, нормальное распределение, другие законы распределения, двумерные случайные величины, функции от случайных величин, ЗБЧ, предельная теорема и т.д.
Пригодится: Более 200 выполненных задач по терверу и Решебники по теории вероятностей.
Где можно найти теорию и формулы по ТВ?
На сайте для вас есть онлайн-учебник по теории вероятностей с краткой теорией и примерами решений.
Пригодится: Формулы и таблицы по теории вероятностей.
Есть ли у вас обучающие видео по терверу?
Да, на странице видеоуроки по ТВ и комбинаторике. Другие полезные материалы и ссылки вы найдете на странице Учебники и ссылки.
Можно ли использовать онлайн-калькуляторы для решения и самопроверки?
Да, вы можете решать задачи и сверять ответы с помощью наших онлайн-калькуляторов по ТВ.
Как научиться решать задачи по теории вероятностей?
Начните с онлайн-учебника по терверу (или того, который рекомендует преподаватель, например, Гмурмана), последовательно изучая теорию и разбирая примеры. У нас на сайте есть цикл обучающих статей по разным типам задач (про монеты, лотереи, станки, задачу о встрече и многое другое). Для проверки можно использовать интерактивные калькуляторы. В разделе Примеры решений найдете решенные задач, разбитые по темам, с подробными пояснениями.
Как оформлять контрольную по теории вероятностей?
Контрольные обычно оформляют в формате Word. В документ включают:
- Задания в том порядке, в котором они даны;
- Подробные решения с формулами, пояснениями и вычислениями;
- Графики, таблицы и диаграммы, если они требуются в решении.
Полезное: гайд по оформлению контрольных работ.
Из каких методичек есть еще готовые работы по теории вероятностей?
В разделе готовых работ по вузам выложены решения:
Если вам нужно выполнить контрольную по вероятности — переходите на страницу решение теории вероятностей на заказ, где подробно описаны цены, сроки, гарантии и формы оплаты. Там же можно оставить заявку и получить быструю оценку стоимости. Также поможем со сдачей теста по теории вероятностей.

