Закон редких событий
Как Пуассон искал справедливость с помощью формул
В истории науки есть удивительные примеры, когда абстрактная математика помогает понять суть глубоко человеческих проблем, такик как справедливость и ответственность. Один из таких примеров связан с именем Симеона Дени Пуассона, французского физика и математика, который в 1837 году сформулировал вероятностный закон, названный впоследствии его именем — распределение Пуассона.
Этот закон стал незаменимым инструментом в самых разных областях: от оценки риска и надёжности до биологии, физики и телекоммуникаций. А началось всё… с размышлений о судебных приговорах.
Суд, ошибки и математика: Франция начала 19 века
Симеон Дени Пуассон (1781–1840) был одним из выдающихся учёных своего времени. Ученик Лапласа, коллега Фурье и Лежандра, он внёс вклад в математический анализ, физику, астрономию. Но одной из его самых неожиданных и в то же время влиятельных работ стала книга:
«Recherches sur la probabilité des jugements en matière criminelle et en matière civile»
("Исследования вероятности судебных приговоров в уголовных и гражданских делах", 1837).
В этой работе Пуассон попытался ответить на, казалось бы, нематематический вопрос: Какова вероятность того, что суд выносит ошибочный приговор, если присяжные (как и все люди) изредка могут ошибаться?
Судебная система того времени включала коллегиальные решения (например, суд присяжных заседателей), и Пуассон рассматривал вероятности голосования за или против обвиняемого. Он рассмотрел малую вероятность индивидуальной ошибки каждого судьи или присяжного, а затем исследовал вероятность совокупной ошибки в решении суда. В книге Пуассон исследовал воздействие изменений в уголовном законодательстве на долю осуждений и на ошибки при осуждениях и оправданиях.
Полный текст книги в переводе О.Б. Шейнина (2013).
Путь к формуле: как родилось распределение Пуассона
Математический аппарат, использованный Пуассоном, опирался на уже существующие на тот момент представления о биномиальном распределении. Оно описывает число успехов в серии независимых испытаний с двумя исходами (как в данном случае: голос может быть дан "за" или "против").
Пуассон задался вопросом: что будет, если число "испытаний" велико (много судебных процессов), но вероятность ошибки присяжного в каждом отдельном случае мала?
Он пришёл к выводу, что в предельном случае биномиальное распределение превращается в новый вид распределения, описывающий вероятность наступления редких событий (в т.ч. судебных ошибок).
Это новое распределение он не называл своим именем — термин "распределение Пуассона" закрепился в литературе позднее. Однако именно его работа заложила основу вероятностного моделирования редких и независимых событий.
Основная формула распределения Пуассона
Пусть:
- \( p \) — вероятность ошибки (или наступления другого редкого события) в одном испытании;
- \( n \) — количество независимых испытаний;
- параметр \( \lambda = n \cdot p \) — среднее (ожидаемое) число ошибок (событий).
Если \( n \to \infty \) и \( p \to 0 \), так что \( \lambda \) остается постоянным (и обычно находится в интервале от 1 до 10), то биномиальное распределение:
$$P(k) = C_n^k \cdot p^k \cdot (1 - p)^{n - k}$$
переходит в распределение Пуассона:
$$P(k; \lambda) = \frac{\lambda^k e^{-\lambda}}{k!}$$
Это распределение описывает вероятность того, что в фиксированном интервале произойдёт ровно \( k \) событий, если события редки и происходят независимо друг от друга.
Пуассон применил эту модель к анализу судебных решений: если в год рассматривается большое число дел, и в каждом вероятность ошибки мала, то общее число ошибочных приговоров подчиняется данному закону.
Где применяется распределение Пуассона сегодня?
С момента своего появления распределение Пуассона стало универсальным инструментом в науке и технике. Его применяют там, где речь идёт о количестве редких событий за фиксированный интервал.
Вот несколько примеров:
- Телекоммуникации: число входящих звонков за минуту
- Физика: число распадов радиоактивных ядер за секунду
- Биология: число случайных мутаций в ДНК;
- Криминология: число краж/преступлений в районе за сутки
- Логистика: поток заказов в течение рабочего дня на складе
- Типография: число опечаток на одной странице текста
- География: число землетрясений в регионе за год с заданной магнитудой;
Это распределение лежит в основе теории массового обслуживания, надежности, страхования, биостатистики и анализа данных в IT.
Сегодня имя Пуассона носят не только распределение, но и уравнение Пуассона в физике, формула Пуассона в теории потенциала, ядро Пуассона в комплексном анализе. Но именно распределение, возникшее из размышлений о суде, стало его самым узнаваемым научным наследием.
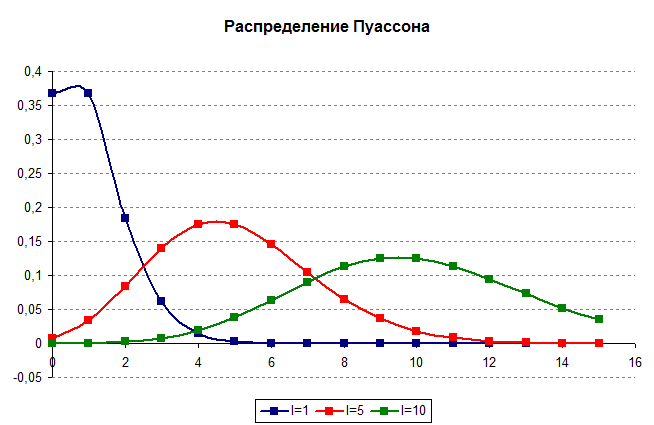
Характеристики и график распределения Пуассона
Рассмотрим некоторый поток событий, в котором события наступают независимо друг от друга и с некоторой фиксированной средней интенсивностью $\lambda$ (событий в единицу времени). Тогда случайная величина $X$, равная числу событий $k$, произошедших за фиксированное время, имеет распределение Пуассона. Вероятности вычисляются по следующей формуле:
$$ P(X=k)=P(k; \lambda)=\frac{\lambda^k}{k!}\cdot e^{-\lambda}, \quad k=0,1,2,... $$Математическое ожидание: $$\mathbb{E}(X) = \lambda$$
Дисперсия: $$D(X) = \lambda$$
Мода: $$Mo= \lfloor \lambda \rfloor \quad \text{или} \quad Mo= \lfloor \lambda \rfloor - 1 $$
Коэффициент эксцесса: $$Ex(X) = \lambda^{-1}$$
График распределения ведет себя по-разному, в зависимости от параметра: при малых \( \lambda \) оно сильно асимметрично (см. синий график, \( \lambda=1 \)), при возрастающих значения \( \lambda \) приближается к нормальному (см. зеленый график, при \( \lambda=10 \) уже имеет характерный вид "колокола").