Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ - количество "успехов" в последовательности из $n$ независимых случайных экспериментов, таких что вероятность "успеха" в каждом из них равна $p$ ("неуспеха" - $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 0 | 1 | ... | k | ... | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^{n-1}$ | $C_n^k \cdot p^k \cdot q^{n-k}$ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$ P(X=k) = C_n^k \cdot p^k \cdot (1-p)^{n-k} = C_n^k \cdot p^k \cdot q^{n-k}, k=0,1,2,...,n. $$Числовые характеристики биномиального распределения:
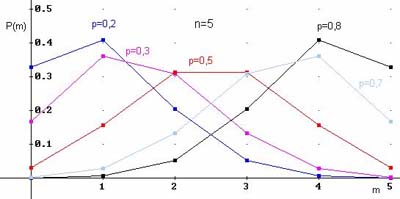
$$M(X)=np, \quad D(X)=npq, \sigma(X)=\sqrt{npq}.$$Примеры многоугольников распределения для $n=5$ и различных вероятностей:
Примеры решенных задач на биномиальный закон ДСВ
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $p\to 0$, $n \to \infty$, $np \to \lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | ... | k | ... |
| $p_k$ | $e^{-\lambda}$ | $\lambda e^{-\lambda}$ | ... | $\frac{\lambda^k}{k!}\cdot e^{-\lambda}$ | ... |
Вероятности вычисляются по формуле Пуассона:
$$ P(X=k)=\frac{\lambda^k}{k!}\cdot e^{-\lambda}, k=0,1,2,... $$Числовые характеристики для распределения Пуассона:
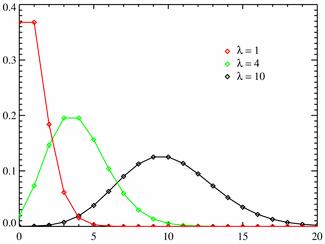
$$M(X)=\lambda, \quad D(X)=\lambda, \sigma(X)=\sqrt{\lambda}.$$Разные многоугольники распределения при $\lambda = 1; 4; 10$.
Примеры решенных задач на закон Пуассона
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ - количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Формула для вероятностей:
$$ P(X=k) = q^k \cdot p, k=0,1,2,...,n,... $$Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | ... | k | ... |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | ... | $q^k \cdot p$ | ... |
Числовые характеристики:
$$M(X)=\frac{q}{p}, \quad D(X)=\frac{q}{p^2}.$$Примеры решенных задач на геометрическое распределение
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n \le N$). Найти закон распределения случайной величины $X$ - равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n \lt K$, то до $n$). Вероятности вычисляются по формуле: $$ P(X=k)=\frac{C_K^k \cdot C_{N-K}^{n-k}}{C_N^n}, \quad 0\le k \le K. $$
Числовые характеристики:
$$M(X)=\frac{K}{N}\cdot n, \quad D(X)=\frac{K}{N}\cdot n \cdot \frac{N-n}{N} \cdot \frac{N-K}{N-1}.$$Примеры задач на гипергеометрическое распределение
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения величины $X$(везде $ \lambda \gt 0)$:
$$ f(x)= \left\{ \begin{array}{l} 0,\ x \lt 0\\ \lambda e^{-\lambda x},\ x\ge 0 \\ \end{array} \right. $$Функция распределения величины $X$:
$$ F(x)= \left\{ \begin{array}{l} 0,\ x \lt 0\\ 1- e^{-\lambda x},\ x\ge 0 \\ \end{array} \right. $$Числовые характеристики можно найти по формулам:
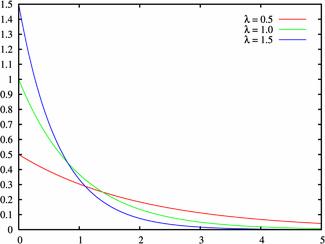
$$M(X)=\frac{1}{\lambda}, \quad D(X)=\frac{1}{\lambda^2}, \quad \sigma= \frac{1}{\lambda}.$$Плотность распределения при различных значениях $\lambda \gt 0$:
Примеры решенных задач на показательное распределение
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
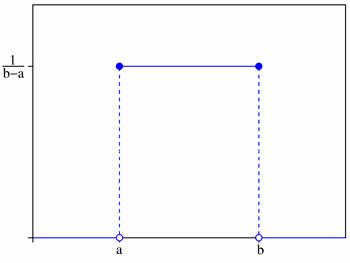
Плотность распределения на отрезке $(a;b)$:
$$ f(x)= \left\{ \begin{array}{l} 0,\ x \le a\\ \frac {1}{b-a},\ a \lt x \le b, \\ 0,\ x \gt b, \\ \end{array} \right. $$Функция распределения:
$$ F(x)= \left\{ \begin{array}{l} 0,\ x \le a\\ \frac {x-a}{b-a},\ a \lt x \le b, \\ 1,\ x \gt b, \\ \end{array} \right. $$Числовые характеристики равномерно распределенной случайной величины:
$$M(X)=\frac{a+b}{2}, \quad D(X)=\frac{(b-a)^2}{12}, \quad \sigma=\frac{b-a}{2\sqrt{3}}.$$График плотности вероятностей:
Примеры решенных задач на равномерное распределение
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Плотность распределения нормальной случайной величины $X$ имеет вид:
$$f(x)= \frac{1}{\sigma\sqrt{2\pi}} \exp\left({-\frac{(x-a)^2}{2\sigma^2}}\right). $$При $a=0$ и $\sigma=1$ эта функция принимает вид:
$$\varphi(x)= \frac{1}{\sqrt{2\pi}} e^{-x^2/2}.$$Скачать таблицу для функции $\varphi(x)$
Числовые характеристики для нормального распределения:
$$M(X)=a, \quad D(X)=\sigma^2.$$Пример графика плотности распределения для различных значений среднего и СКО:
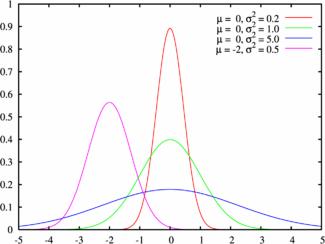
Нормальный закон распределения случайной величины с параметрами $a=0$ и $\sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.
Функция Лапласа определяется как:
$$\Phi(x)= \frac{1}{\sqrt{2\pi}}\int_0^x e^{-t^2/2} dt$$Скачать таблицу для функции Лапласа
Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(\alpha, \beta)$:
$$ P(\alpha \lt X \lt \beta) = \Phi\left( \frac{\beta-a}{\sigma} \right) - \Phi\left( \frac{\alpha-a}{\sigma} \right). $$Вероятность отклонения нормально распределенной случайной величины $X$ на величину $\delta$ от математического ожидания (по модулю).
$$ P(|X -a|\lt \delta) = 2 \Phi\left( \frac{\delta}{\sigma} \right). $$Примеры решенных задач на нормальное распределение
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:

