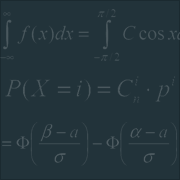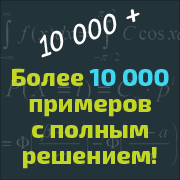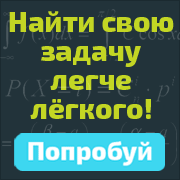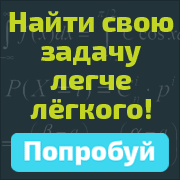Задачи о беспорядках
На этой странице мы разберемся с тем, что же такое беспорядок в математике, кто его изобрел;) и как подсчитать количество беспорядков (да, их много;)). Рассмотрим классическую задачу Эйлера о шляпах, выведем формулу для числа беспорядков (субфакториал), укажем другие полезные формулы и свойства, и, конечно, разберем еще несколько задач (о письмах, о контрольных), которые решаются аналогично и часто встречаются в учебниках.
Что такое беспорядок?
Беспорядок (англ. Derangement) — это перестановка чисел от 1 до n, в которой ни один элемент не стоит на своём месте.
Для $n=1$ беспорядков нет (единица стоит на своем единственном месте всегда),
для $n=2$ получаем только один беспорядок: (21),
для $n=3$ существует два беспорядка: (231) и (312),
для $n=4$ - уже девять: (2143), (2341), (2413), (3142), (3412), (3421), (4123), (4312), (4321).
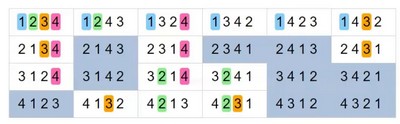
На картинке выше перечислены все 4!=24 перестановки 4 цифр. Цветным подсвечены те места, где цифры на своих местах, а серым выделены варианты, когда каждая цифра - на чужом месте, то есть серые ячейки - это как раз беспорядки.
Но, чем больше n, тем сложнее выписывать беспорядки непосредственно, и тем больше становится их число, например, для $n=10$ их уже больше миллиона! (ниже вы найдете таблицу с числом беспорядков для первых натуральных n)
Впервые задачу поиска количества беспорядков для n-элементного множества поставил Пьер Де Монмор в 1708 году, и в 1713 нашел ее решение (с помощью аналога современной формулы включений и исключений). Но чаще всего, когда говорят о беспорядках, вспоминают задачу Эйлера о шляпах.
Задача Эйлера
Задача (Леонид Эйлер) Войдя в ресторан, n гостей оставили швейцару свои шляпы, а на выходе получили их обратно. Швейцар раздал шляпы случайным образом. Сколько существует вариантов, при которых каждый гость получит чужую шляпу?
Рассмотрим классическое решение данной задачи, использующее формулу включений и исключений: для любых конечных множеств $A_1$, $A_2$,..., $A_n$ справедливо равенство
$$ |A_1 \cup A_2 \cup ... \cup A_n |=\sum_i |A_i|- \sum_{i\lt j}|A_i\cap A_j| + \sum_{i\lt j \lt k}|A_i\cap A_j \cap A_k| +...\\ +(-1)^{n+1} |A_1\cap A_2 \cap A_3 \cap ... \cap A_{n}|. $$Примеры решенных задач на принцип включений и исключений можно найти тут
Обозначим гостей и шляпы цифрами от 1 до n, при этом считаем, что i-му гостю принадлежит i-ая шляпа. Перестановка вида $k_1 k_2 ... k_n$ обозначает ситуацию, когда $i$-ый гость получил шляпу с номером $k_i$. Всего перестановок будет $n!$, нас интересуют только те, которые являются беспорядками, их количество можно найти, вычтя из общего числа те перестановки, где хотя бы одно число стоит на своем месте (шляпа выдана хозяину), то есть $k_i=i$.
Пусть $A_i$ - множество перестановок, в которых число $i$ стоит на своем месте ($i=1,2,...,n$). Тогда число беспорядков есть
$$ N=n!-|A_1 \cup A_2 \cup ... \cup A_n |=\\ = n!-\sum_i |A_i|+ \sum_{i\lt j}|A_i\cap A_j| - \sum_{i\lt j \lt k}|A_i\cap A_j \cap A_k| +...+(-1)^{n} |A_1\cap A_2 \cap A_3 \cap ... \cap A_{n}|. $$Мощность $A_i$ - количество перестановок, в которых число $i$ стоит на своем месте, можно подсчитать так: зафиксировать это число, а все остальные числа переставлять всеми возможными уже $(n-1)!$ способами. То есть, $|A_i|=(n-1)!$. Тогда $\sum_i |A_i| =n\cdot (n-1)!=n!$.
Аналогично, $|A_i\cap A_j| =(n-2)!$, и тогда
$$ \sum_{i\lt j}|A_i\cap A_j| =C_n^2 \cdot (n-2)!=\frac{n!}{2!(n-2)!}\cdot (n-2)!=\frac{n!}{2!}. $$Далее находим $|A_i\cap A_j\cap A_k| =(n-3)!$,
$$ \sum_{i\lt j \lt k}|A_i\cap A_j\cap A_k| =C_n^3 \cdot (n-3)!=\frac{n!}{3!(n-3)!}\cdot (n-3)!=\frac{n!}{3!}. $$Продолжая, придем к следующей формуле для числа беспорядков:
$$ N=n!-n!+\frac{n!}{2!}-\frac{n!}{3!}+...+(-1)^{n-1}\frac{n!}{(n-1)!}+(-1)^n =n! \cdot \sum\limits_{k=0}^{n}\frac{(-1)^k}{k!} $$Это и есть искомое число вариантов, при которых каждый гость получит чужую шляпу, или число беспорядков. Частные случаи мы разберем ниже в примерах задач.
Формулы. Субфакториал. Свойства
Количество беспорядков множества из $n$ элементов равно субфакториалу числа $n$ (обозначается $!n$) и вычисляется по формуле:
$$ !n=n! \left( 1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1)^n\frac{1}{n!} \right)= n! \sum\limits_{k=0}^{n}\frac{(-1)^k}{k!} \quad(*)$$Рекуррентное соотношение для нахождения количества беспорядков
Количество беспорядков $d(n)$ удовлетворяет рекурсивным соотношениям: $$d(n)=(n−1)\left[d(n−1)+d(n−2) \right]$$ $$d(n)=n \cdot d(n−1)+(−1)^n, \quad d(1)=0, d(2)=1$$
Их же можно записать как cвойства субфакториала, которые используются для упрощения формул и вычислений:
$$!n=(n−1)\left[!(n−1)+!(n−2) \right]$$ $$!n= !(n−1)\cdot n +(−1)^n. $$Другие формулы вычисления субфакториала
$$ !n=\frac{\Gamma(n+1,-1)}{e}, \quad \text{где } \Gamma \text{ - неполная гамма-функция} $$ $$ !n= \left[\frac{n!}{e}\right], \quad \text{где } [x] \text{ - ближайшее целое число к } x.$$Рост числа беспорядков
Из основной формулы (*) для числа беспорядков и разложения экспоненты $exp(x)=\sum_{k=0}^{\infty}\frac{x^k}{k!}$, подставляя $x=1$ легко получить, что
$$ \lim\limits_{n \to\infty}\frac{!n}{n!} = \lim\limits_{n \to\infty} \sum\limits_{k=0}^{n}\frac{(-1)^k}{k!} =exp(-1) \approx 0,3679.$$То есть вероятность того, что произвольная перестановка $n$-элементного множества окажется беспорядком, стремится к постоянному значению $1/e$ (при возрастании $n$).
Число беспорядков для первых натуральных n
| $n$ | $!n$ |
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 9 |
| 5 | 44 |
| 6 | 265 |
| 7 | 1854 |
| 8 | 14 833 |
| 9 | 133 496 |
| 10 | 1 334 961 |
| 11 | 14 684 570 |
| 12 | 176 214 841 |
| 13 | 2 290 792 932 |
| 14 | 32 071 101 049 |
| 15 | 481 066 515 734 |
Примеры задач о беспорядках с решениями
Задача о шляпах. Гардеробщица одновременно выдала номерки 6 лицам, сдавшим в гардероб свои шляпы, и повесила их наугад. Найти вероятность того, что каждый получит собственную шляпу? Найти вероятность, что каждый получит чужую шляпу?
Используем классическое определение вероятности: $p=M/N$ , где $M$ – число исходов, благоприятствующих осуществлению события, а $N$ – число всех равновозможных элементарных исходов. $N=6!=720$ - число различных способов выдать номерки 6 людям.
$M_1=1$ - только один способ соответствует ситуации, когда каждый получит свою шляпу (свой номерок). Искомая вероятность для первого вопроса задачи $p_1=1/720\approx 0,0014.$
Рассмотрим второй вопрос задачи. Число благоприятствующих исходов для события "каждый получит чужую шляпу" равно числу беспорядков $M_2=!6=6! \sum_{k=0}^{6}\frac{(-1)^k}{k!} = 265$, тогда вероятность $p_2=265/720\approx 0,368$.
Помимо задачи о шляпах, классическими стали постановки еще двух, использующих беспорядки, задач: о рассеяной секретарше (задача о письмах) и о хитром профессоре (задача о контрольных). Рассмотрим их ниже.
Задача о письмах. Секретарше нужно отправить n различных писем по n различным адресам. Она подписывает конверты и, по рассеяности, случайным образом вкладывает письма в конверты. Какова вероятность того, что ни одно письмо не дойдет до своего адресата? Какова вероятность, что хотя бы одно письмо придет по адресу?
Очевидно, что здесь мы снова имеем задачу о беспорядках. Известно, что всего способов вложить письма в $n$ конвертов будет $n!$, то вероятность, что они все будут по чужому адресу (то есть благоприятствующие исходы - $!n$ беспорядков), равна
$$ \frac{!n}{n!} = \sum\limits_{k=0}^{n}\frac{(-1)^k}{k!}.$$Вероятность, что хотя бы одно письмо придет по адресу, тогда равна
$$ 1-\frac{!n}{n!} = 1-\sum\limits_{k=0}^{n}\frac{(-1)^k}{k!}.$$Например, для случая 5 писем, получим соответственно, 0,3667 и 0,6333.
Задача о контрольных. Профессор дал n студентам контрольную, а затем предложил им проверить ее друг у друга. Ни один студент не должен проверять свою контрольную. Сколько у профессора вариантов распределения контрольных?
И снова задача напрямую сводится к поиску числа беспорядков - вариантов распределения контрольных, при которых каждый студент получит чужую работу. Ответ - $!n$ вариантов, частные случаи см. выше в таблице.
Возможны и другие постановки задач, которые вы, прочитав эту статью, легко сможете решить:
- Пятеро членов семьи приготовили на праздник 5 подарков, а затем устроили случайный обмен внутри семьи. Сколькими способами они могут обменяться подарками так, чтобы никто не получил свой собственный?
- Почтальон Печкин очень переживал о судьбе Дяди Федора и в задумчивости разнес 10 посылок по 10 домам в Простоквашино наугад. Какова вероятность того, что хотя бы один адресат получит свою посылку?
- Задача Монмора. Две колоды карт, одну из которых заранее хорошенько перетасовали, сравниваются карта за картой. Какова вероятность того, что, открывая одновременно в обеих колодах карту за картой, мы не встретим ни одного совпадения?
Полезные ссылки
- Вычисление субфакториала на разных языках программирования (Java, C, C#, Python, Javascript): Коды (листинги) программ
- Интересное решение задачи о письмах через графы
- Онлайн-калькуляторы по комбинаторике
- Видеоролик о беспорядках: примеры задач о беспорядках, формула для решения, задача о шляпах.
Решебник по вероятности
В решебнике вы найдете тысячи решенных задач по теории вероятностей: