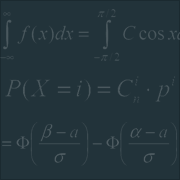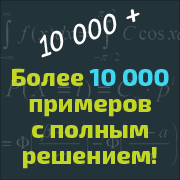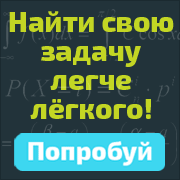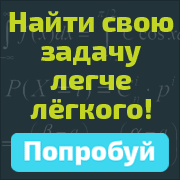Случайные функции

Случайные процессы - довольно редкая тема в курсе теории вероятностей (не все до нее доходят), но все-таки приведем несколько примеров решений типовых задач.

Обычно в заданиях требуется найти характеристики случайной функции: математическое ожидание, корреляционную функцию, дисперсию. Также нужно уметь находить характеристики процесса, который зависит от другого (чаще всего зависимость выражается интегралом, производной или задается дифференциальным уравнением).

Далее: Примеры решений для стационарных случайных процессов.

Примеры решений

Задача 1. Найти $m_X(t), K_X(t_1,t_2), D_X(t)$, если $X(t)=U \cdot e^{-t^2}$, где $U$ - случайная величина с характеристиками $m_U=5, D_U=0,001$.

Задача 2. На вход интегрирующего устройства поступает случайный процесс $X(t)$ с характеристиками: $$m_X(t)=t^2-5, K_X(t_1,t_2)=2\sin 3t_1 \sin 3t_2.$$ Найти $m_Y(t), K_Y(t_1,t_2), D_Y(t)$, если $$Y(t)=t^2 \int_0^t X(\tau)d\tau +3t.$$

Задача 3. Найти числовые характеристики производной случайной функции, если

$$m_{\xi}(t)=\cos 7t, \quad K_{\xi}(t_1, t_2) = 7t_1 t_2 +1/7 t_1^4 t_2^4.$$

Задача 4. Случайная функция $X(t)$ задана каноническим разложением $X(t)=t^2+t+Z\cos 3t +V e^2t$, где $D_Z=1$, $D_V=3$. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции $Y(t)=\frac{dX(t)}{dt}+2-t$.

Задача 5. Дан случайный процесс $Y(t)=X \cos(t)$, $t \gt 0$, где $X$ - нормально распределенная величина с параметрами $m_x$ и $\sigma_x$. Найти корреляционную функцию и нормированную корреляционную функцию случайного процесса.

Задача 6. Найти взаимную корреляционную функцию $R_{xy}(t_1, t_2)$ и взаимную нормированную корреляционную функцию $\rho_{xy}(t_1, t_2)$ двух случайных функций $X(t)=A\sin t + B \cos t$ и $Y(t)=A e^t +Be^{-t}$, если известно, что дисперсии случайных величин $A$ и $B$ равны: $DA=4$, $DB=4$, коэффициент ковариации $cov(A,B)=-4$.

Задача 7. Случайная функция $X(t)$ имеет автоковариационную функцию $K_x(t,t')=e^{t-2t'}$. Найти автоковариационную функцию случайной функции $Y(t) = \int_0^t X(\tau) d \tau$.